Extreme-mass-ratio inspirals (EMRIs)

EMRIs are astrophysical binaries composed of a stellar-mass compact object (with a mass about the mass of the Sun) gradually inspiralling into a massive black hole (with a mass 1000 to 10 million times the mass of the Sun). They will emit long-lasting millihertz gravitational waves, making them ideal sources for the upcoming spaced-based gravitational wave detector: the Laser Interferometer Space Antenna (LISA). By measuring the gravitational wave signals of distant EMRIs, astrophysicists will learn about the environments and internal dynamics of stellar clusters and galactic centers, measure the the expansion of the universe, and test general relativity by precisely measuring the quadrupole moments of spinning astrophysical black holes.

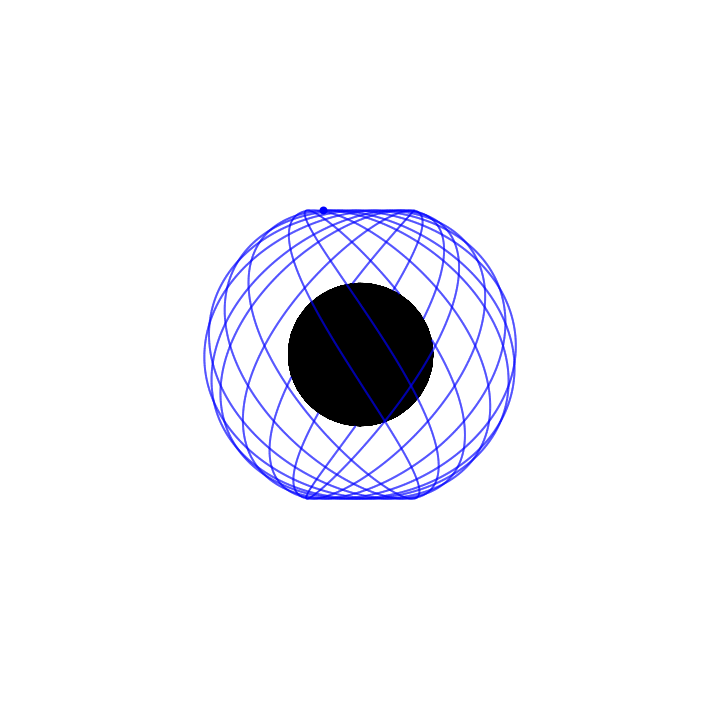
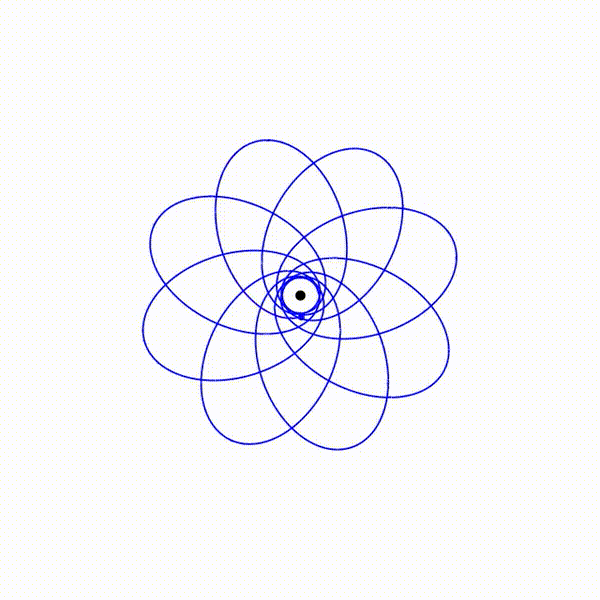
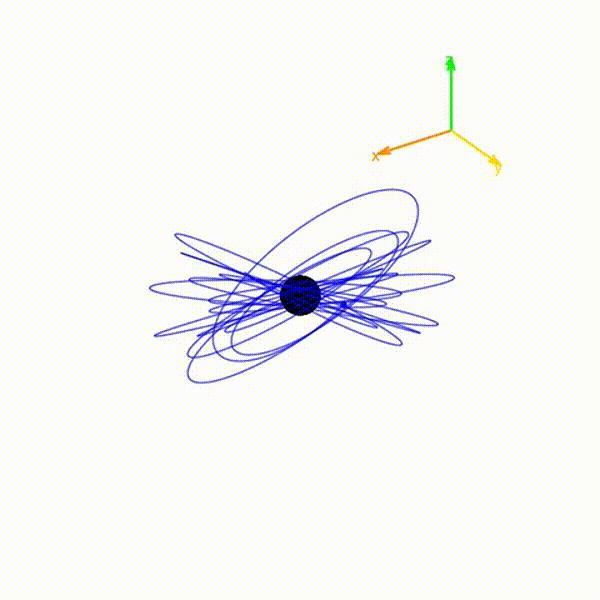
EMRI resonances

As most EMRIs evolve, they will eventually pass through particular orbital configurations known as resonances. Resonances occur when at least two frequencies of motion form a (relatively prime) integer ratio. Resonances that form between the azimuthal motion and the other orbital frequencies (i.e., \(r\phi\)- and \(\theta\phi\)-resonances) lead to the anisotropic radiation of gravitational waves, leading to kicks to an EMRI's center of mass. On the other hand, resonances that form between the radial and polar motions of the system (i.e., \(r\theta \)-resonances) will enhance or diminish the rate at which an EMRI radiates away energy and angular momentum through gravitational waves. This latter effect will have a strong impact on EMRI gravitational wave signals. Therefore, it is important to improve our models of EMRIs as they pass through \(r\theta\)-resonances, because they can hinder the ability of LISA to accurately detect and characterize EMRI signals.

For more information about my research on EMRI resonances, see my latest contributed talks here.

Quasinormal bursts (QNBs)

QNBs are faint, periodic high-frequency oscillations that appear in EMRI waveforms. These oscillations arise in an EMRI when its smaller body follows a highly eccentric orbit that brings it through successive close encounters with the more massive primary black hole. QNBs get their name because they can be mapped to the quasinormal mode frequency spectrum of rotating Kerr black holes. Thus they are a physical signal produced by the small body effectively "ringing" the larger black hole and the surrounding spacetime by its repeated periaspsis passages.

For more information about my research on EMRI QNBs, see my latest paper here.